Flood In The Jungle
Jan 16, 2019 16:55 · 1099 words · 6 minute read
Flood in the Jungle (100 Marks)
A group of monkeys are living in Sunderbans forests. There are N trees in Sunderbans (numbered from O to N-l) on which these monkeys live. Every year floods hit the forest of Sunderbans The monkeys have a tradition of meeting on a tree after the flood. Last night Sunderbans has been hit hard by a sudden flood. The flood was very strong and it has submerged everything except the mighty trees on which the monkeys live. 1 9 All the monkeys now have to meet on some tree. Due to the flood the trees have become weak so jumping from them is dangerous. Whenever a monkey jumps fro m a tree A to a tree B, the tree A gets submerged a little while the tree B remains unaffected. monkeys don’t know how to swim. So, they move from one tree to another tree by jumping Every tree has been assigned a 2D - coordinate value. A monkey can only jump between two trees if the euclldean distance between them is less than or equal to C. C IS called the jumping capacity of the monkeys. The trees have threshold values. The threshold value of the ith tree is given by ti. It means that no more than ti monkeys can jump off from
The trees have threshold values. The threshold value of the ith tree is given by ti. It means that no more than ti monkeys can jump off from the ith tree. You are given the coordinates of the trees, their threshold values, the number of monkeys on the trees, and the jumping capacity of the monkeys. You have to tell the number of the trees on which the all monkeys can meet after the flood. The meeting can happen on a tree if all the monkeys can come to this tree.
Input Format
- The first line of input contains 2 integers N and C, denoting the number of trees and the jumping capacity of the monkeys.
- Following N lines contains xi yi mi ti - the x-coordinate of the ith tree, the y-coordinate of the ith tree, the number of monkeys on the ith tree and the maximum number of monkeys that can jump off from the ith tree.
- The last line of the input is kept blank.
Constraints
- 1 <= N <=200
- 0 <= C<= 100,000
- -100,00 <= xi,yi <= 100,00
- 0 <= mi <= 15,
- 1 <= ti <=200
Output Format
One line with space separated integers denoting the numbers of the trees on which the meeting can happen. These numbers should be in ascending order and should be from O to N-l. If there IS no tree on which the meeting can happen then print -1
Sample Test Case 1
Input
3 100.0
1 10 5 5
5 10 5 1
8 10 5 4
Output
-1
Explanation
There are 5 monkeys on the 1st tree (0-based indexing) while only 1 can jump off this tree. Similarly, there are 5 monkeys on the 2nd tree but only 4 can jump off So, there is no tree where all the monkeys from the 1st tree and 2nd tree can meet Hence, answer IS -1 Note that trees are numbered from 0 to 2.
Sample Test Case 2
Input
3 100.0
1 10 5 20
5 10 5 20
8 10 5 20
Output
0 1 2
Explanation
The meeting can happen on all the trees
Solution
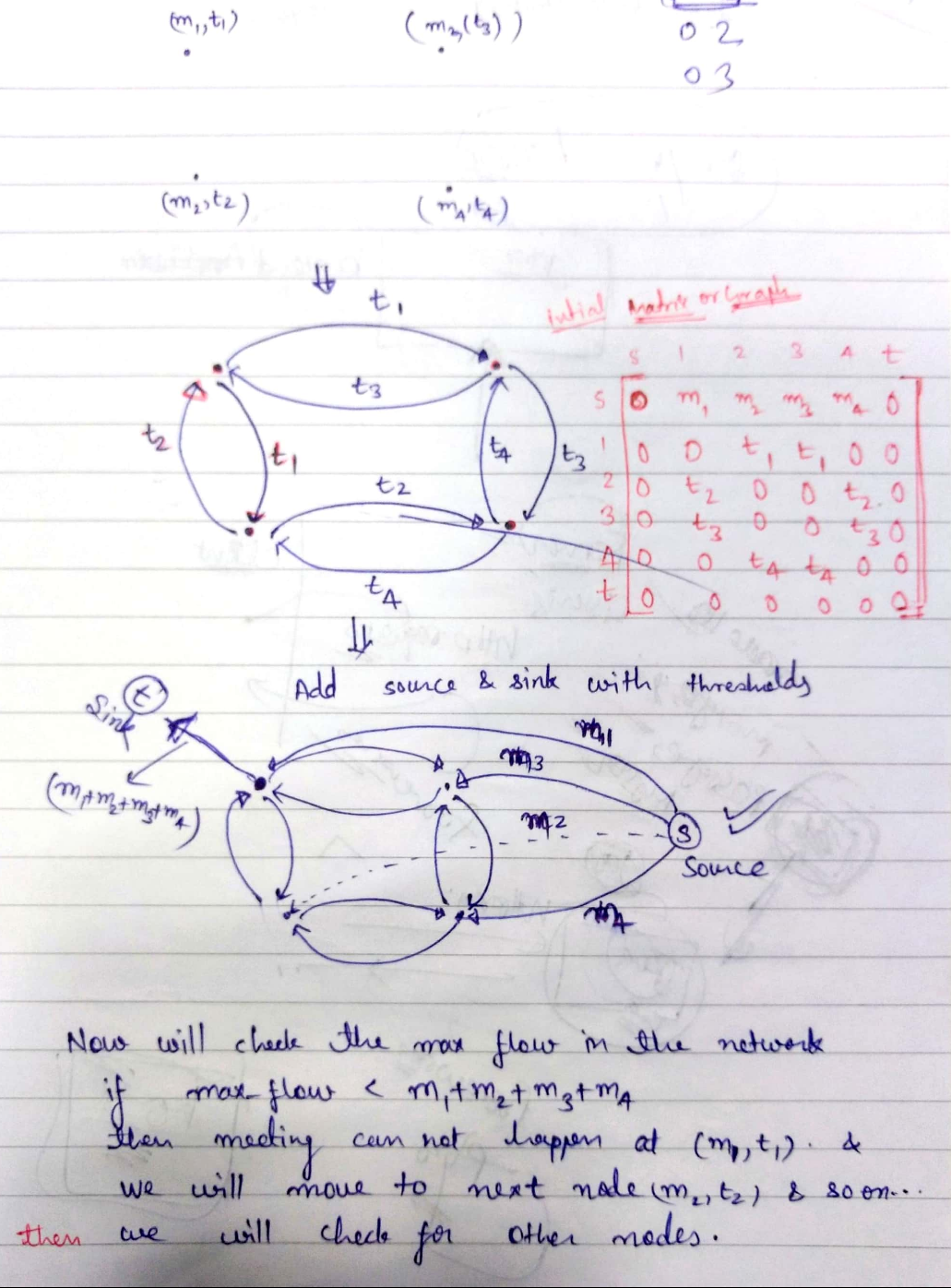
Solution to problem in Python is as follows:
import collections
import copy
# This class represents a directed graph using adjacency matrix representation
def dist(l, m):
return (posAppendList[l][0] - posAppendList[m][0]) ** 2 + (posAppendList[l][1] - posAppendList[m][1]) ** 2
def graph1Generator():
for i in range(len(connectedTrees)):
newGraph[connectedTrees[i][0]][connectedTrees[i][1]] = thrList[connectedTrees[i][0]-1]
for j in range(0, numTree):
newGraph[0][j + 1] = monList[j]
return newGraph
# This class represents a directed graph using adjacency matrix representation
class Graph:
def __init__(self, graph):
self.graph = graph # residual graph
self.ROW = len(graph)
def BFS(self, s, t, parent):
'''Returns true if there is a path from source 's' to sink 't' in
residual graph. Also fills parent[] to store the path '''
# Mark all the vertices as not visited
visited = [False] * (self.ROW)
# Create a queue for BFS
queue = collections.deque()
# Mark the source node as visited and enqueue it
queue.append(s)
visited[s] = True
# Standard BFS Loop
while queue:
u = queue.popleft()
# Get all adjacent vertices's of the dequeued vertex u
# If a adjacent has not been visited, then mark it
# visited and enqueue it
for ind, val in enumerate(self.graph[u]):
if (visited[ind] == False) and (val > 0):
queue.append(ind)
visited[ind] = True
parent[ind] = u
# If we reached sink in BFS starting from source, then return
# true, else false
return visited[t]
# Returns the maximum flow from s to t in the given graph
def FordFulkerson(self, source, sink):
# This array is filled by BFS and to store path
parent = [-1] * (self.ROW)
max_flow = 0 # There is no flow initially
# Augment the flow while there is path from source to sink
while self.BFS(source, sink, parent):
# Find minimum residual capacity of the edges along the
# path filled by BFS. Or we can say find the maximum flow
# through the path found.
path_flow = float("Inf")
s = sink
while s != source:
path_flow = min(path_flow, self.graph[parent[s]][s])
s = parent[s]
# Add path flow to overall flow
max_flow += path_flow
# update residual capacities of the edges and reverse edges
# along the path
v = sink
while v != source:
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
# my code goes here
numTree, monCap = input().split()
numTree = int(numTree)
monCap = float(monCap)
posAppendList = [];
monList = [];
thrList = []
for i in range(0, numTree):
x = [int(i) for i in input().split()]
posAppendList.append([x[0], x[1]])
monList.append(x[2])
thrList.append(x[3])
connectedTrees=[]
for i in range(0, numTree):
for j in range(0, numTree):
if not ((float(dist(i, j)) > monCap ** 2) or (i == j)):
connectedTrees.append([i+1,j+1])
source = 0;
treeCount = 0
totalMon=sum(monList)
newGraph = [[0 for x in range(numTree + 2)] for y in range(numTree + 2)]
newGraph = graph1Generator()
for i in range(0, numTree):
newGraph[i + 1][numTree + 1] = totalMon
#graph=copy.deepcopy(newGraph)
g = Graph(newGraph)
sink = i + 1
val = g.FordFulkerson(source, sink)
if val == totalMon:
print(sink - 1, end=" ")
treeCount += 1
newGraph = graph1Generator()
if (treeCount == 0):
print("-1")
This problem is from Second round of Techgig Code Gladiators 2018. Where i made it to finals.